Dans le chapitre précédent, vous avez vu comment tracer le spectre d'un signal.
L'idée de ce chapitre est de modifier un peu le signal dans sa représentation spectrale et de voir l'effet que cela aura sur la représentation temporelle.
Acquisition des données et obtention des paramètres importants
Vous trouverez les données à utiliser
Le fichier que vous utilisez est un vrai son, vous pouvez d'ailleurs l'écouter avec votre lecteur audio favori.
%Acquisition des données audio
[SonStereo Fe] = audioread('violon.wav'); %Fe est la fréquence d'échantillonnage (44100 Hz est une fréquence souvent utilisée pour les fichiers sonores)
SonMono = SonStereo(:,1);
% SonStereo a deux colonnes car le son a été enregistré sur deux voies. Ne prenez que la première voie.
N = length(SonMono); % le nombre de points du signal
Te = 1 / Fe; % durée entre deux échantillons
Vous l'avez sans doute remarqué, une musique stéréo ne correspond pas qu'à un seul signal. Il y en a en fait deux, un pour chaque haut-parleur.
Nous n'allons travailler que sur une seule voie et nous travaillerons finalement qu'avec un son mono.
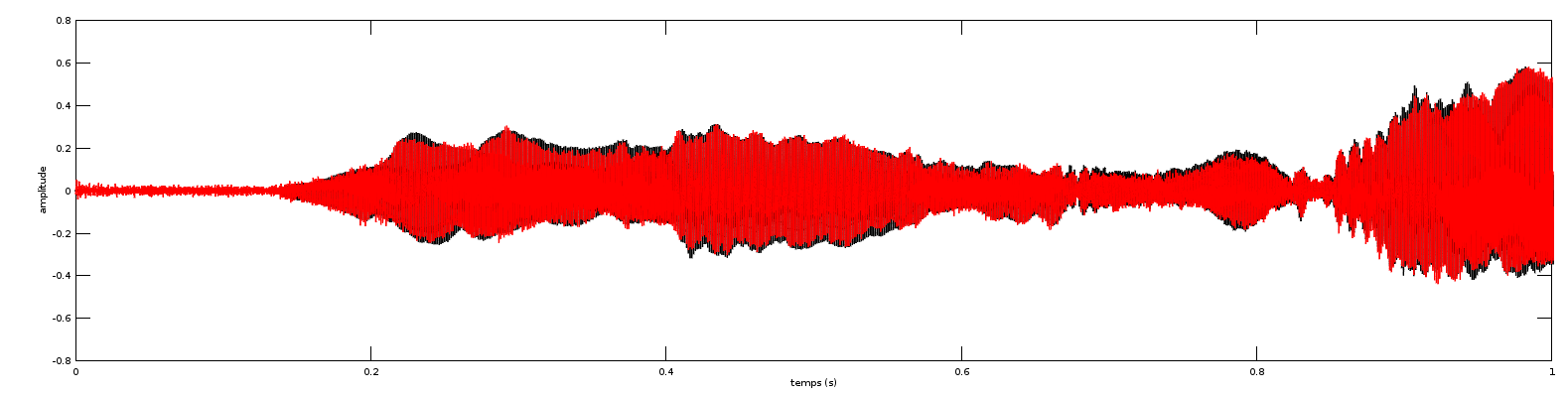
Si vous voulez, vous pouvez visualiser le son en utilisant :
t = [0:Te N-1)*Te]; % temps (part de 0, avance de Te en Te, et contient N points
N-1)*Te]; % temps (part de 0, avance de Te en Te, et contient N points
plot(t,sonMono); %tracé de l'amplitude du HP en fonction du temps
Vous remarquerez alors qu'un son, en représentation temporelle, correspond à des oscillations (en fait les oscillations de la membrane du micro ou bien du haut-parleur) plus ou moins rapides au cours du temps et dont l'amplitude varie.
Obtention du spectre
Puisque nous avons le nombre de points et la durée d'échantillonnage vous pouvez d'ores et déjà savoir à quoi correspondra l'espace des fréquences (voir chapitre précédent) :
Freq = [0:N-1]/(N*Te); %l'espace des fréquences
Et vous devriez savoir qu'il est possible d'obtenir sa transformée de Fourier facilement avec la fonction fft de Matlab.
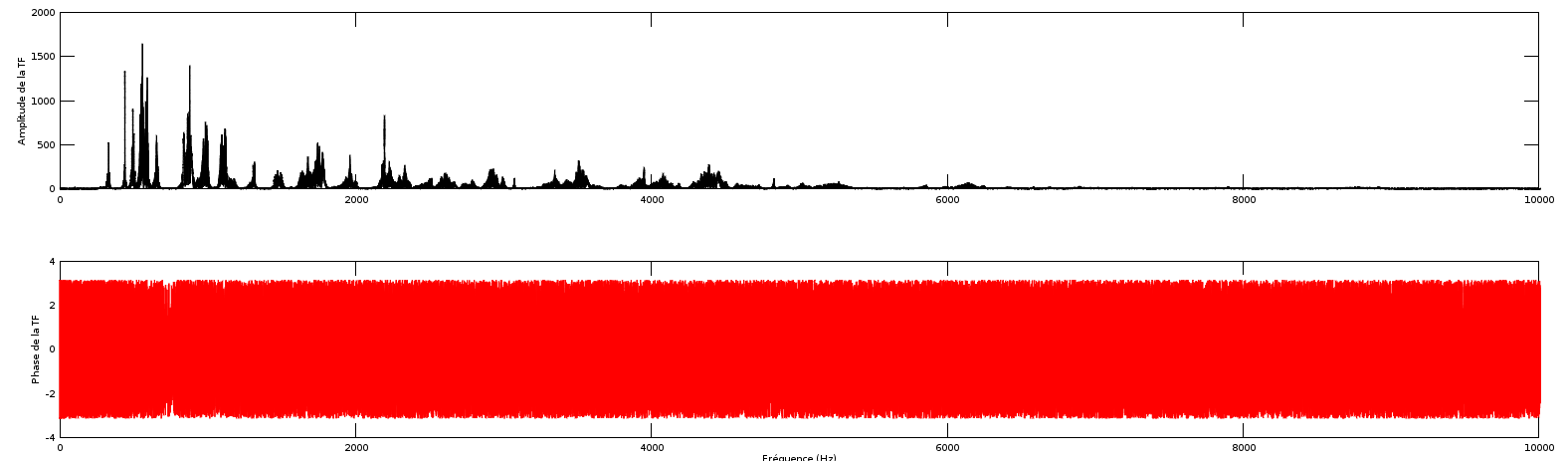
%représentation fréquentielle
subplot(2,1,1)
plot(Freq, abs(tf),'k') % tracé de l'amplitude en fonction de la fréquence
xlim([0 10000])% on se limitte aux fréquences <10 kHz
subplot(2,1,2)
plot(Freq, arg(tf),'r')
% tracé de la phase en fonction de la fréquence
xlim([0 10000])