Qu’est-ce qu'un signal ?
Pour commencer ce cours, je vais préciser ce dont je vais vous parler.
Il est important de définir précisément les termes que je vais employer, car derrière des mots utilisés dans la vie courante se cachent des définitions physiques qui ne sont pas forcément en accord avec votre interprétation de ces mots.
Comprenez bien que si vous n'entendez pas la même chose que ce qui est dans ces définitions, ce n'est pas que vous avez tort, c'est simplement que la physique a fait le choix de définir ces notions d'une façon et non pas d'une autre.
Le signal dans le langage courant
Dans le sens commun et de manière informelle, un signal est une information qui peut parfois varier
dans le temps ou l’espace. Par exemple, vous pouvez penser à :
- Un son, une chanson, un discours radiophonique.
- Une image, une photo, un tableau, un film.
- De façon plus générale, tout ce qui fait appel à vos sens : une odeur, mais aussi une sensation d’équilibre, la perception de son propre corps, la sensation de faim, etc.

Ci-dessus un signal g(x,y) bi-dimensionnel, représentant une intensité de gris en fonction de x et y, aussi connu sous le nom de "image". Piranesi, Carceri Plate XI – The Arch with a shell ornament
Le signal d'un point de vue physique
En physique, la notion de signal est beaucoup plus restrictive ! La physique va restreindre la notion de signal aux grandeurs que vous pouvez représenter de façon mathématique. Donc, cette définition
très réductrice ne prend pas en compte la diversité des moyens couramment appelée "signal" et qui vous
permet de communiquer de l’information.
Définition
Un signal est une grandeur ou une collection de grandeurs issue(s) d’un capteur ou d’une collection de capteurs.
Exemples de signaux
Dans la liste suivante, le nombre associé au signal sera noté
et la dépendance de ce signal est mise entre parenthèses.
La dimensionnalité du signal correspond au nombre de ces dépendances.
- Signal 1-D : u(t), par exemple un signal sonore issu d’un microphone.
- Signal 2-D : u(x,y), par exemple une image en niveaux de gris issue d’un capteur CCD (capteur photographique).
- Signal 3-D : u(x,y,z), par exemple une image tridimensionnelle issue d’un scanner ou bien u(x,y,t), un film issu d’une caméra.

Un film sans piste sonore est simplement une valeur de niveau de gris g, qui dépend de x,y et t. g(x,y,t). C'est un signal 3-D.
-
Signal 4-D : u(x,y,z,t), par exemple le flux issu d’un jeu vidéo en réalité virtuelle.
-
Signal N-D : u(x1,x2,...,xN), le flux issu de N captures (réseau de capteurs).
Un exemple récurrent : signal 1-D
Tout au long du cours, je prendrai souvent pour exemple une série de température, car c'est un exemple concret et pratique.
Regardez par exemple les variations de températures à New-York au début de l'année 1989 :
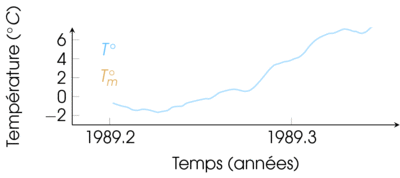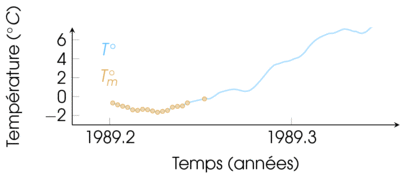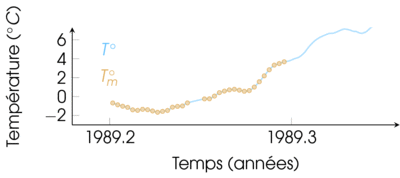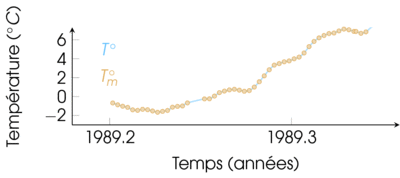
Encore par souci de simplification, ici je vous montrerai uniquement des signaux échantillonnés régulièrement.
"Traiter" un signal ?
Traiter un signal, c'est effectuer des opérations mathématiques pour retirer des informations qui sont intéressantes (qui font sens) pour un être humain, à partir du signal de base.
Vous pouvez par exemple vous intéresser à la valeur moyenne, médiane, à la distribution, aux valeurs minimum et maximum (ce sont là des propriétés statistiques).
Mais vous pouvez imaginer vouloir accéder à un autre point de vue sur un signal. Au lieu de le voir sous la forme d'une évolution temporelle, vous pourriez vous intéresser à l'aspect répétitif ou non du signal. Vous pouvez également vous demander si un motif apparaît dedans, etc.
Conclusion
- Un signal au sens physique est simplement une représentation mathématique d'une grandeur.
- Le nombre de paramètres qui font varier un signal détermine la dimensionnalité du signal.
- Traiter un signal, c'est faire des opérations mathématiques sur le signal de base pour obtenir d'autres grandeurs intéressantes.
Maintenant que vous savez ce qu'est un signal (au sens physique), je vais vous expliquer comment le quantifier !


