Analysez les signaux 1D: Tricher à "Où est Charlie ?"

Comment tricher à "Où est Charlie ?"

Pour clore ce cours, je vous propose de traiter une image, qui est un signal 2D.

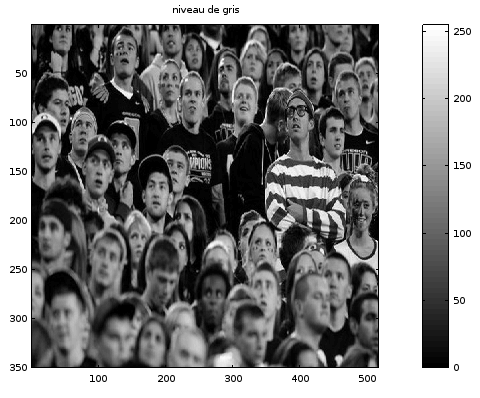
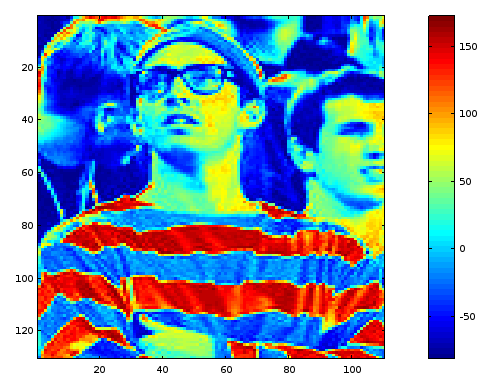
Vous connaissez peut-être le jeu "Où est Charlie ?" ? Il s'agit d'un jeu où le but est de retrouver un petit personnage en t-shirt rayé blanc et rouge au sein d'une autre grande image.

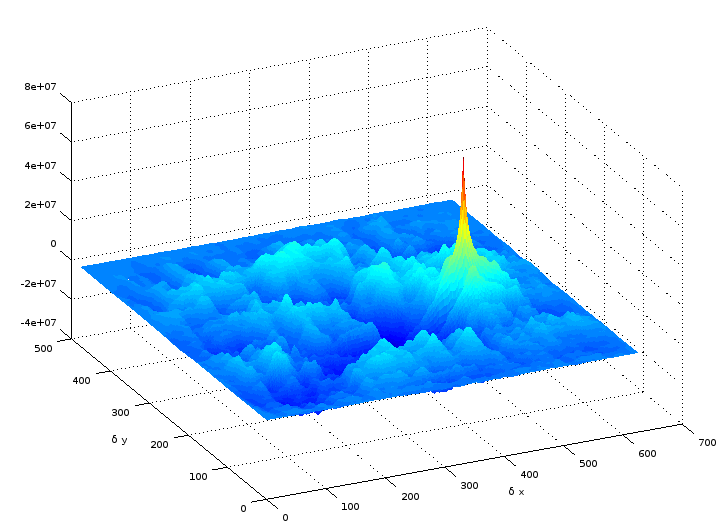
L'essentiel du jeu consiste à passer en revue l'intégralité de l'image au peigne fin. Je vous propose de tricher, en utilisant justement l'inter-corrélation.

Le but sera donc le suivant, retrouver Charlie dans cette image :

Où est charlie? Attention c'est très dur. ( Jonathan Ferrey / Getty Images)

Où est charlie? Attention c'est très dur. ( Jonathan Ferrey / Getty Images)

Acquisition

Commencez par enregistrer cette image sur votre ordinateur, appelez-la "waldo.png". Notez qu'il s'agit d'une image de 518 pixels de large sur 350 de haut.

Ensuite il vous faut importer cette image dans Octave:


        %pkg load image; % A décommenter si vous travaillez sous linux
%pkg load signal; % A décommenter si vous travaillez sous linux
clear
I = imread("waldo.png"); % chargement de l'image
figure(1);
imshow(I); % visualisation de l'image
whos
            I; % On demande à octave plus d'info sur I

Cette dernière commande : "whos" vous permet d'obtenir un peu plus de détail sur la nature de I.




>> whos I
Variables in the current scope:

 Attr Name      Size       Bytes   Class
 ==== ====      ====       =====   ===== 
       I      350x518x3    543900   uint8

L'information importante à lire ici est la colonne "size". L'objet I est un tableau de taille 350 x 518 x 3, c'est-à-dire qu'en fait, il s'agit de 3 tableaux de taille 350 x 518. Chaque tableau correspond à une valeur de niveau de Rouge, de Vert et de Bleu correspondant à chaque pixel.

Traiter les images couleur est encore un tout petit peu trop dur, donc nous allons transformer cette image en niveau de gris. Nous n'aurons plus qu'un seul tableau.


Ig = rgb2gray(I); % Ig correspond à I mais en niveau de gris
Ig = double(Ig); % transforme le type de Ig de uint8 vers double, pour oublier les soucis de division.

Ig est maintenant une simple matrice de valeurs étalées entre 0 et 255. Pour visualiser les valeurs d'une matrice, vous pouvez utiliser la commande imagesc (ou image).

Visualisation


  
    figure(2)
imagesc(Ig); %Visualisation des valeurs de la matrice 
colormap('gray'); %assure que le code couleur est en niveau de gris
colorbar; %affiche l'échelle des couleurs
title('niveau de gris')

Vous obtenez alors :

Une matrice peut être visualisée avec la commande imagesc

L'image à rechercher

Chargez les données du fichier waldo_seul.dat.


        waldo = load('waldo_seul.dat'); % on charge l'image à rechercher
figure(3)
imagesc(waldo); % on visualise cette matrice
colorbar; % Echelle de couleur

Vous obtenez :

La matrice que nous allons rechercher. Par défaut, l'échelle de couleur n'est pas une échelle de gris, mais une échelle allant du bleu au rouge. Si vous voulez une échelle de gris, il vous faudra rajouter la commande: colormap('gray')

Pas besoin d'être un génie pour reconnaître que cette image se trouve en fait aux alentours de la position (100/400) dans l'image originale.

Mais comme d'habitude, nous allons automatiser les choses avec l'inter-corrélation.

Inter-corrélation entre deux images

Ici, nous allons inter-corréler deux matrices. Mathématiquement, il n'y a rien de compliqué.

Définition mathématique

Nous allons étendre la notion d'inter-corrélation. Cette fois le signal ne dépend pas du temps , mais il dépend de $t$ et , et au lieu d'avoir un seul paramètre de décalage $ \tau $ , il y en aura deux : $ \delta_{x} $ et $ \delta_{y} $.

On appellera inter-corrélation bi-dimensionnelle la grandeur , telle que :

$ \Gamma[I_{1}, I{2}](\delta x, \delta y) = \iint{I_{1}(x,y) I_{2}(x - \delta x, y - \delta y) dx dy} $

Implémentation

Si ce n'est pas très clair, ce n'est pas bien grave. Le point important à comprendre ici est que rien ne change sur le sens du résultat. La valeur de l'inter-corrélation sera d'autant plus grande que l'image $ I_{1} $ ressemble à l'image $ I_{2} $ lorsqu'il y a le bon décalage.


        Ig0 = Ig - mean(mean(Ig)); % petite subtilité, pour avoir un résultat encore plu
s net, il faut supprimer la valeur moyenne des signaux que l'on intercorrelle
correlation = xcorr2(Ig0,waldo); % xcorr2 est l'implémentation octave de l'inter
correlation
            2D
            
figure(4)
s = surf(correlation);% visualisation du résultat sous forme de surface
set(s,'edgecolor','none'); % cosmétique

Et vous obtenez :

Résultat de l'Inter-corrélation 2D.

Alors comment interpréter ce résultat ?

Vous pouvez voir que la matrice "correlation" possède un pic en ( $ δx≈460 $ et $ δy≈200 $ $δ y \approx 200$ ).

Et si vous revenez à l'image de départ, vous verrez qu'il s'agit bien de la position du coin en bas à droite de la vignette que nous recherchions dans l'image de départ.

Malheureusement, il n'y a pas l'équivalent de lag pour xcorr2. Si vous voulez avoir les positions de façon automatique, utilisez :


                [r,snd] = max(correlation();
[positionX,positionY] = ind2sub(size(correlation),snd)

Conclusion

Alors, à l'issue de ce chapitre, savez-vous vraiment tricher à "Où est Charlie?" ?

Si vous deviez appliquer cette méthode au vrai jeu, vous vous rendrez rapidement compte que l'inter-corrélation n'est pas un outil miraculeux. Des petites variations dans l'orientation, dans l'angle de vue ou encore dans l'échelle rendront cet outil moins performant. Mais il s'agit souvent d'un bon point de départ.

Voilà qui achève ce cours. J'espère que vous en savez plus sur ce qui est communément appelé le "traitement du signal".

Si pour vous la notion de spectre n'est pas magique comme elle l'est souvent pour beaucoup d'étudiants, alors bravo à vous ! N'hésitez pas à briller en société en évoquant ce sujet lors des soirées mondaines.