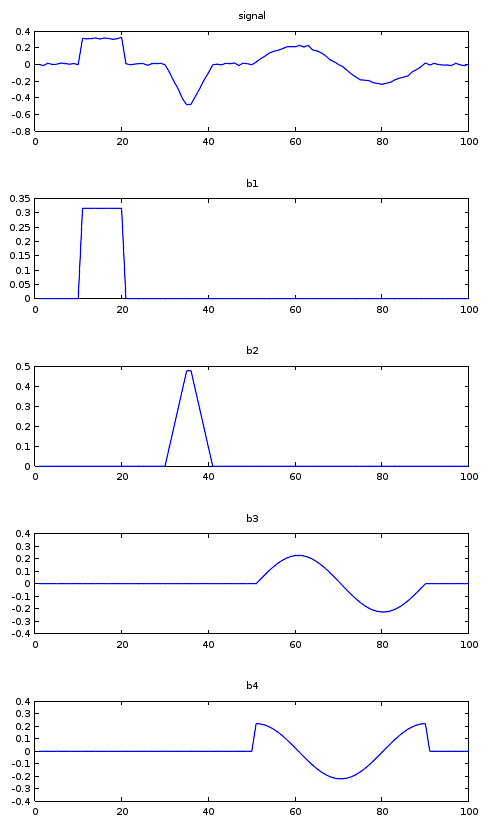
Ce n'est pas une énorme surprise : comme b1 et b2 ont des valeurs non nulles à des endroits strictement différents, chaque terme du produit scalaire fera intervenir une multiplication par 0. La somme totale est donc nulle.
Là où l'on pourrait être plus sceptique, c'est pour b3 et b4 qui ont des valeurs non nulles au même endroit. Le produit scalaire de ces deux vecteurs risque donc d'être non nul.
Certes, ce n'est pas tout à fait nul, mais c'est très petit. Donc, on pourra considérer que ces deux vecteurs sont quasiment orthogonaux et cela ne devrait pas trop affecter notre décomposition.
Plus exactement,
\( ⟨\overrightarrow{b_{3}}\overrightarrow{b_{4}}⟩≪⟨\overrightarrow{b_{3}},\overrightarrow{b_{3}}⟩=1 \) . Dire qu'une grandeur est petite n'a de sens que lorsqu'elle est négligeable devant une autre grandeur de référence.
Vous allez dire : "c'est un peu un miracle tout ça".
Eh bien, pas tant que ça. Les deux signaux b3 et b4 n'ont pas été choisis au hasard. Comme vous le remarquerez surement, il s'agit dans un cas d'un sinus et dans l'autre d'un cosinus de même période. Et le tout pris sur une période complète.
Or, si vous vous rappelez de vos cours de maths, vous vous souviendrez sûrement (ou pas du tout  ) que :
) que :
\( \int_{0}^{2 \Pi } sin(x)cos(x)dx=0 \)
Donc, ce n'est pas tant que ça un miracle.
Vous pouvez vérifier que toutes les combinaisons possibles des vecteurs de base qui vous sont fournis sont orthogonales.
Nous avions donc bien des vecteurs de base orthonormés.
Y-t-il autant de vecteurs de base que la taille de l'espace ?
Enfin, pour que vous soyez assuré de recomposer le signal complètement, il faut autant de vecteurs de base que la taille de l'espace.
Or ici, la taille de l'espace est le nombre de points, il y en a N = length(signal), soit dans notre cas : 100.
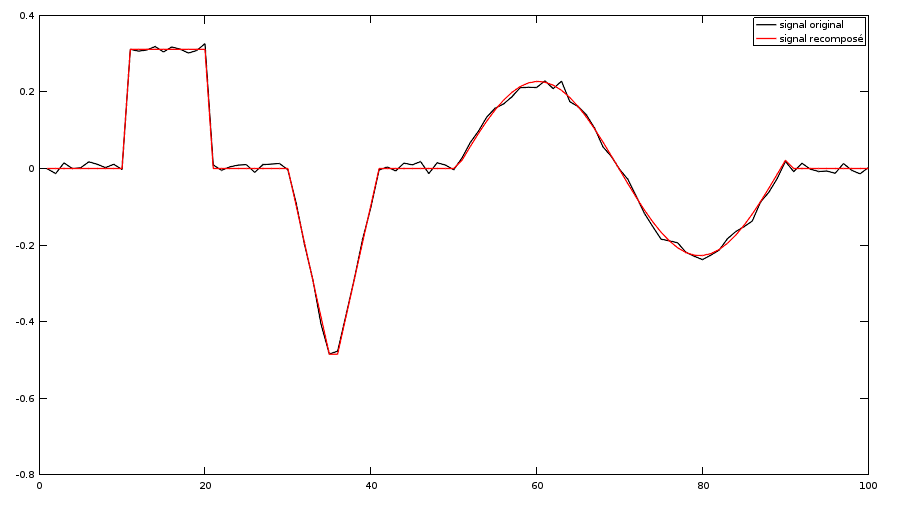
Nous n'avions que 4 vecteurs de base, c'est donc bien insuffisant pour pouvoir constituer une base complète, c'est d'ailleurs pour cela qu'il y a au final une différence entre le signal reconstitué et les données.
Conclusion
Vous venez de recomposer un signal à partir d'éléments de base. Pour le moment, ces éléments de base étaient visuellement faciles à reconnaître (triangle, carré, vague) mais ils ne sont pas très utilisés pour le reste des signaux.
Dans la suite du cours, vous allez voir que les signaux de base en forme de sinusoïdes sont particulièrement intéressants.

 ) que :
) que :
