Analysez les signaux 1D: Évaluer un modèle

Évaluer un modèle

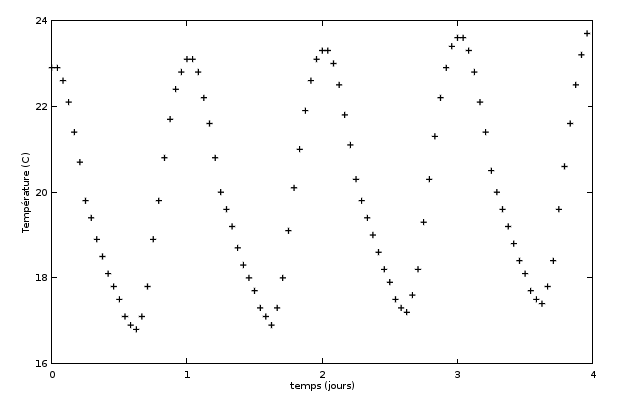
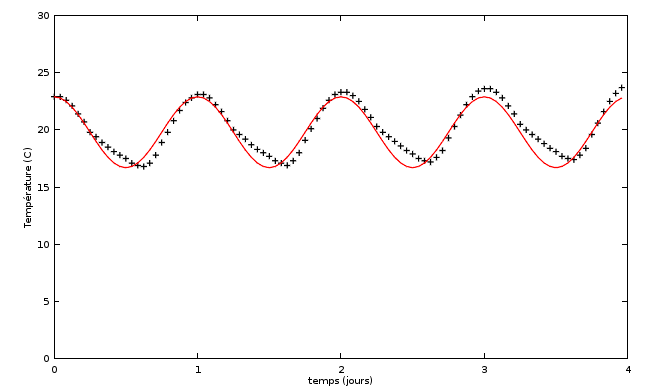
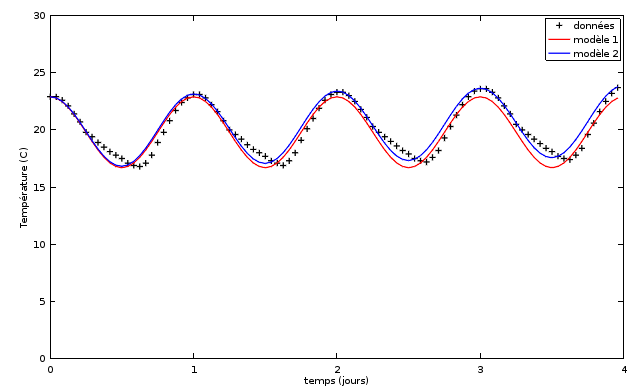
Illustrons la notion de distance sur un exemple numérique (à traiter sous Octave). Pour cela, nous allons utiliser la distance vue dans la partie précédente pour évaluer quantitativement la différence entre des données expérimentales et un modèle théorique d'évolution des températures.

Vous trouverez dans le fichier data.dat un relevé horaire de températures sur une durée de trois jours.

Importation et représentation

Commençons par importer les données sous Octave :


                                            %Importation des données
data = load('data.dat');
%La première colonne correspond au temps
t = data(:,1);
%La deuxième colonne correspond au données
Temp = data(:,2);

Le fichier data.dat doit se trouver dans le répertoire de travail ("current directory", commande pwd dans la console) . Vous devrez déterminer/changer ce répertoire dans la fenêtre qui se situe sous la barre des menus.

Zone qui précise le répertoire de travail.

Une fois les données importées, nous pouvons les visualiser :


        %Tracé de la température en fonction du temps (ramené en jours), option 'k+' pour avoir des marqueurs noirs en forme de croix verticale.
plot(t/(60*24),Temp,'k+');
%Nom des axes
xlabel('temps (jours)');
ylabel('Température (C)');

Vous devriez obtenir :

Représentation des données

Une première analyse

On remarque que les températures oscillent de façon journalière (avec une période de $ T=1 $ jour) autour d'une température d'environ $ T{m}≈20^{\circ} C $et avec une amplitude proche de $a \approx 3^{\circ} C$ .

En voyant cela, on pourrait naturellement imaginer que la température suit la loi mathématique suivante :

$ T_{model1}=T_{m}+a⋅cos(\frac{2π}{T}t) $

Afin de tester cette hypothèse, nous allons la comparer ce modèle à l'expérience, en les représentant tous les deux sur un même graphique.


        %construction du modèle:
model1 = 19.8 + 3.1*cos(2*pi*(1/(24*60))*t);
%Représentation du modèle sur le même graphique en rouge ('r')
hold on
plot(t/(60*24),model1,'r')
hold off
%l'autoscale sur l'axe vertical est trompeur, forçons
            la représentation à montrer les données sur l'intervalle 0 30 degrés
ylim([0 30])

Vous devriez obtenir :

Représentation des données et du modèle

Représentation des données et du modèle

On constate donc que le modèle et la réalité sont relativement en accord, même si le modèle semble assez mauvais la nuit.

Même si l'argument visuel a du sens. Nous n'avons toujours pas mis de nombre sur la différence entre le modèle et la réalité.

Distance

Toutes ces considérations sont finalement assez subjectives et si l'on souhaite avoir une mesure quantitative, la distance entre les deux signaux est un outil possible.

La distance que l'on utilise ici n'est pas le seul outil quantitatif possible. Il existe une multitude de façons de comparer des signaux. Il ne faudra pas être trop hâtif dans les conclusions que l'on tirera de ce critère.

La distance euclidienne entre le signal théorique et le signal expérimental est définie par :

$ d = \sqrt{ \sum_{i=1}^n (T_{model}(i)-T_{exp}(i))^2 } $

C'est ce que nous avons vu dans la partie précédente.

Pour obtenir cette valeur numériquement vous pouvez procéder de façon suivante :


                        %différence point à point
model1-Temp
%carré de la différence: attention le . devant ^ est important, sans quoi matlab tente de faire un produit de matrice.
(model1-Temp).^2)
%Somme de chacun des termes
sum((model1-Temp).^2)
%Finalement,
                            pour voir la distance souhaitée, on prend la racine (square root)
dist1 = sqrt(sum((model1-Temp).^2))

On obtient alors une distance de $ 7.3238 $. À ce stade, il est difficile d’interpréter ce nombre. La seule chose pertinente que l'on peut dire, c'est que celui-ci n'est pas nul ; il y a donc une différence entre les données et l'expérience : super, beaucoup de bruit pour rien finalement...

Une analyse plus fine (?)

Pour mieux comprendre cette distance, imaginons un autre modèle, un peu plus fin, qui prendrait en compte le fait que la température semble augmenter progressivement sur les quatre jours (d'environ un degré sur quatre jours).
Ce modèle serait :

$ T_{model2}=(T_{m}+α⋅t)+a⋅cos(\frac{2π}{T}t) $

avec $ α≈ \frac{1 degré}{4 jours} $

On procède de façon similaire en construisant ce modèle numériquement et en évaluant la distance entre les données et ce deuxième modèle :


                                model2 = 19.8 + (1/(24*4*60))*t+3.1*cos(2*pi*(1/(24*60))*t);
dist2 = sqrt(sum((model2-Temp).^2))

On trouve alors une distance de $ 6.7001 $ $6.7001$ ce qui est inférieur à la distance précédente. Vous pouvez donc dire avec certitude et sans subjectivité qu'avec votre critère quantitatif, le modèle 2 est plus proche des données expérimentales que le modèle 1. Ce qui n'est pas forcément évident de façon visuelle.

Visuellement, les deux modèles sont sensiblement équivalents

Visuellement, les deux modèles sont sensiblement équivalents

Conclusion

L'outil distance vous a donc permis de construire un nombre qui permet d'évaluer la différence entre deux signaux.

Ce nombre n'a pas grande signification seul.
Cette distance prend tout son sens lorsqu'elle est comparée à une autre distance avec un autre signal.