Concevez un demi-additionneur
Bonjour et bienvenue dans ce cours ! Dans cette première partie, nous vous proposons de découvrir les principaux circuits arithmétiques permettant d'additionner, de soustraire et de multiplier les nombres binaires. C'est parti !
Concevez un demi-additionneur
Bonjour et bienvenue dans ce cours ! Dans cette première partie, nous vous proposons de découvrir les principaux circuits arithmétiques permettant d'additionner, de soustraire et de multiplier les nombres binaires. C'est parti !
Additionnez les nombres binaires
Considérons deux entiers non signés de 8 bits, A et B. Ces nombres sont compris entre 0 et 255. L'addition arithmétique des deux nombres est donnée dans l'équation ci-dessous :
S=A+B.
Pour obtenir l'addition arithmétique de ces nombres, nous construisons des circuits élémentaires qui réalisent l'addition arithmétique au niveau du bit, comme décrit ci-dessous. L'addition au rang i de deux bits "ai" et " bi" génère un résultat "si" et une retenue "ci" que l'on place sur la colonne suivante (rang i+1).
Pour générer l'addition des deux entiers non signés de 8 bits, nous devons prendre en compte le bit de retenue pour chaque colonne. Pour cela, on crée un circuit avec trois entrées logiques ai, bi et ci-1 pour produire si et ci.
L'additionneur de la colonne 0 est un circuit plus simple qui réalise l'addition de deux données logiques a0 et b0, appelé demi-additionneur.
Dans l'exemple ci-dessus, pour additionner deux
entiers non signés de 8 bits, il faudra utiliser 7 additionneurs complets et un demi-additionneur.
Concevez un additionneur 2 bits à base de portes logiques
La table de vérité et le schéma de principe de la porte demi-additionneur (half-adder) sont illustrés à la figure ci-dessous. Lorsque A et B sont tous deux égaux à 1, la retenue vaut 1 et la somme vaut 0. La combinaison de la retenue (Carry) et de la somme (Sum) est dans ce cas égale à 0b10 en binaire, ce qui équivaut à 2 au format entier.
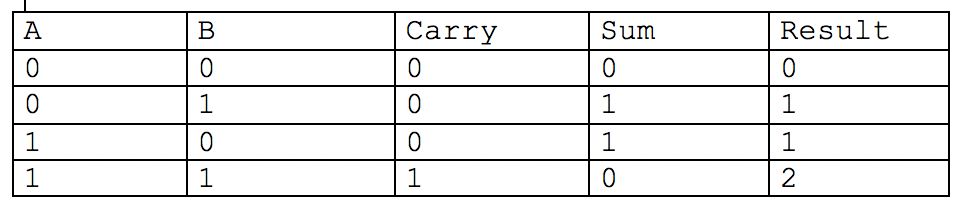
La fonction Sum est créée avec une porte XOR, la fonction Carry par une simple porte AND.
Apprenez à hiérarchiser vos circuits
Lorsque vous concevez un circuit complexe, il peut être intéressant de hiérarchiser certaines fonctions combinatoires si vous devez les utiliser à plusieurs reprises pour votre circuit final.
La démarche de hiérarchisation de circuits à l'aide de l'outil DSCH est explicitée dans le chapitre 5 de cette partie de cours.
Dans ce chapitre, vous avez découvert la brique de base des circuits arithmétiques. Il s’agit de l’addition de 2 bits. Dans le chapitre suivant, vous allez réutiliser ces concepts pour étendre l'addition à n bits.


