L'intercorrélation
L'intercorrélation une première approche
Vous avez vu dans le chapitre précédent que la convolution pouvait s'avérer bien utile. Dans ce chapitre, vous allez découvrir un outil très similaire à la convolution qui s'appelle l'inter-corrélation.
Elle permet, parmi d'autres utilités, de détecter automatiquement un motif.
Introduction
Dans la première partie du cours, vous avez vu que pour comparer des signaux vous pouviez utiliser la distance.
Mais, si deux signaux sont extrêmement ressemblants, mais juste décalés horizontalement, cette distance sera non nulle.
Acquisition et visualisation
Prenez l'exemple des signaux \( s_{1} \) et \( s_{2} \) que vous trouverez ici :
%acquisition des données
s1 = load('s1.dat');
s2 = load('s2.dat');
%Visualisation
plot(s1); hold on ; plot(s2,'r'); hold off
legend({'s_1' 's_2'})
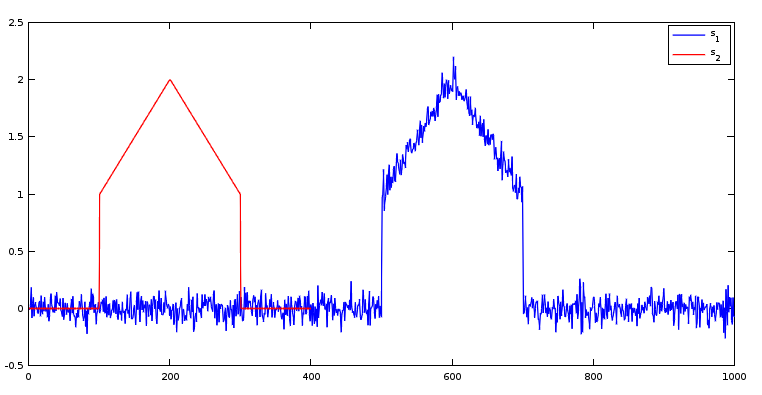
Le signal (en rouge) en forme de maison est bien visible dans le signal (en bleu)
On aimerait bien avoir un outil qui permette de comparer des signaux, tout en s'autorisant un décalage horizontal. C'est le rôle de l'inter-corrélation.
Une pause théorique
Distance entre deux signaux décalés
Imaginez donc que vous souhaiteriez retrouver le motif \( s_{2} \) au sein du signal automatiquement.
Rien de plus simple, ce qu'il faut faire c'est calculer la distance entre les deux signaux, mais avec un paramètre de décalage \( \tau \) .
\( d[s_{1}, s_{2}](\tau) = \begin{Vmatrix} \overrightarrow {s_{1}} - \overrightarrow {s_{2}} (décalé\ de\ \tau) \end{Vmatrix} \)
La distance sera alors minimale pour la valeur de \( \tau \) qui correspond à la position du motif \( s_{2} \) caché dans \( s_{1} \).
Et si vous développez un peu cette expression vous trouverez que :
\( d(\tau) ={\begin{Vmatrix} \overrightarrow {s_{1}} \end{Vmatrix}}^2 + {\begin{Vmatrix} \overrightarrow {s_{2}}(décalé\ de\ \tau) \end{Vmatrix}}^2 - 2<\overrightarrow {s_{1}}, \overrightarrow {s_{2}}(décalé\ de\ \tau) > \)
Définition de l'intercorrélation
Or, ce qui nous intéresse, finalement, c'est de minimiser la distance \( d \) en fonction de \( \tau \).
Comme ni \( \begin{Vmatrix} \overrightarrow{s_{1}} \end{Vmatrix} \) ni \( \begin{Vmatrix} \overrightarrow{s_{2}}(décalé\ de\ \tau) \end{Vmatrix} \) ne vont varier, avec \( \tau \), le problème revient finalement à maximiser \( <\overrightarrow{s_{1}}, \overrightarrow{s_{2}}(t)> \)
Or, si l'on se souvient que décaler un signal, c'est effectuer une translation temporelle :
\( s_{2}(décalé\ de\ \tau) = s_{2}(t-\tau) \) vous comprendrez pourquoi on a introduit ce que l'on appelle l'inter-corrélation de \( s_{1} \) avec \( s_{2} \) :
\( Γs_{1},s_{2}(\tau) = \int{s_{1}(t) s_{2}(t-\tau) d\tau} \)
C'est lorsque cette fonction est maximale que les deux signaux se ressemblent le plus.
Implémentation
La fonction Matlab qui calcule cette grandeur s'appelle xcorr. La fonction Matlab renvoie deux arguments : le premier est l’inter-corrélation elle-même et le deuxième est la valeur
du décalage.
%Calcul de l'intercorrelation
%pkg load signal % a décommenter si vous travaillez sous linux
[gamma lag] = xcorr(s1,s2); % intercorrelation entre s1 et s2
plot(lag, gamma);
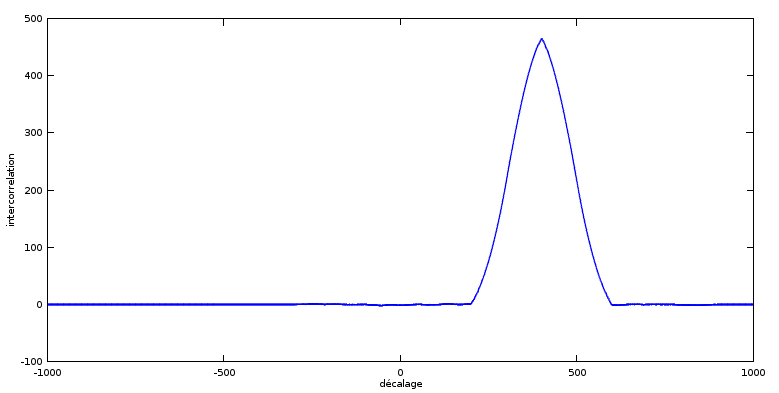
Et assurément, l'intercorrélation est maximale lorsque le décalage vaut 400. Vous pouvez vérifier que si vous décalez le signal \( s_{2} \) rouge
de 400 vers la droite dans la figure de départ, vous trouvez bien la position du motif dans le signal \( s_{1} \) .


