Analysez les signaux 1D: La convolution ?

Qu'est-ce qu'une convolution ?

Que fait donc la convolution ?

Définition mathématique

Mathématiquement, la convolution est une opération mathématique qui prend deux signaux en entrée ( $ u_{1} $ et $ u_{2} $ ) et qui renvoie un nouveau signal $s$ , tel que :

$ s(t) = \int_{-\infty}^{+\infty}{u_{1}( \tau )u_{2}(t-\tau)d\tau} $

Comme la convolution opère sur deux variables d'entrée et qu'elle est très reliée à la multiplication, on utilise souvent le symbole $ \ast $ $*$ pour symboliser cette opération :

$ s=u_{1} \ast u_{2} $

Définition visuelle

Plutôt que de continuer avec des grands discours, vous allez voir directement visuellement ce que fait la convolution.

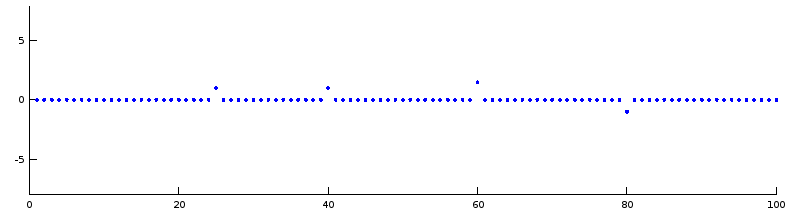
Commencez par créer un signal quasiment nul partout, mais avec quelques valeurs non nulles par-ci par là :


    u1 = zeros(100,1); % Un vecteur avec que des zeros
u1([25;40]) = 1; % on fixe la valeur de u1 à 1 pour les indices 55,128,302 et 50
u1(60)=1.5; %u1 vaut 1.5 pour l'indice 60 
u1(80) = -1; %u1 vaut -1 en 80

plot(u1,'.') % on regarde
        parce que c'est joli
axis([0 100 -8 8]) % fixe la zone de traçage (un peu comme xlim, et ylim en une seule commande

Vous obtenez :

Le signal est non nul en quelques valeurs éparses.

Vous pouvez ensuite créer le deuxième signal, $ u_{2} $ $u_{2}$ et je vous propose de lui donner une forme de trapèze :


            u2 = [0;0;0;5;5;5;5;4;3;2;1;0];%u2 est un signal avec trois zeros, puis une rampe qui descend de 5 jusqu'à zero
plot(u2,'r')

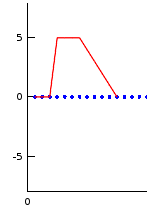
Le signal u2 a une forme de trapèze.

Enfin vous pouvez obtenir la convolution de $u_{1}$

$u_{1}$

 $u_{1}$ s = conv(u1,u2); %s est la convolution de u1 avec u2
plot(s,'color',[0.5 0 0.5]); %On précise la couleur en RGB: 50% rouge, 50% bleu
            
            
            
            
            
        
         $u_{1}$

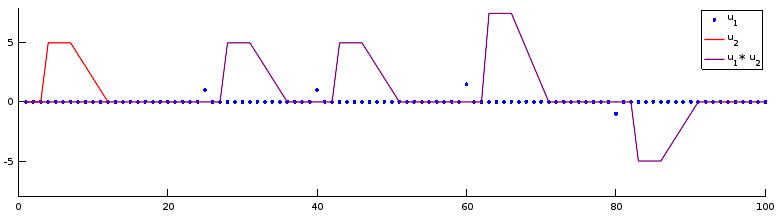
La convolution en mauve.

La convolution en mauve.

Comment interpréter ce résultat ?

Le signal rouge a été recopié partout où le signal bleu était non nul. L'amplitude du recopiage dépend de la valeur du signal bleu. En particulier, si le signal bleu était négatif, le signal rouge est recopié vers le bas (négativement).

Que se passe-t-il si le signal bleu est non nul pour des endroits proches ? Dans ce cas, les signaux recopiés s'ajoutent (où se retranchent) et le résultat de la convolution est plus dur à interpréter visuellement :

clf
u1 = zeros(100,1); % Un vecteur avec que des zeros
u1([25;35;40]) = 1; % on fixe la valeur de u1 à 1 pour les indices 55,128,302 et 50
u1(60) = 1.5; %u1 vaut 1.5 pour l'indice 60 
u1(63) = -0.5;
u1(70) = -1;
u1(80) = -1;
            %u1 vaut -1 en 80
plot(u1,'.','DisplayName','u_1') % on regarde parceque c'est joli
box off
axis([0 100 -8 8]) % fixe la zone de traçage (un peu comme xlim, et ylim en une seule commande
hold on
u2 = [0;0;0;5;5;5;5;4;3;2;1;0];%u2
            est un signal avec trois zeros, puis une rampe qui descend de 5 jusqu'à zero
plot(u2,'r','DisplayName','u_2')
s = conv(u1,u2);
plot(s,'color',[0.5 0 0.5],'DisplayName','u_1\ast u_2')
legend(gca,'show')
hold off

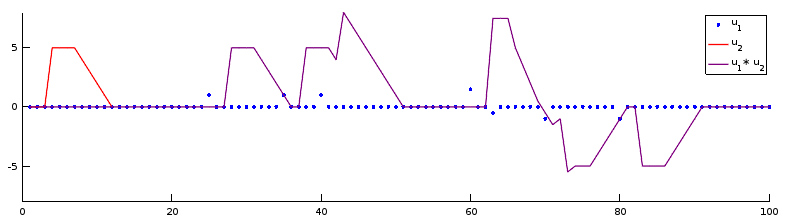
Si les valeurs non nulles de $u_{1}$ sont peu espacées, les recopiages s'ajoutent et se retranchent. Ce qui rend le résultat de la convolution dur à interpréter.

Moyenner et lisser un signal

Moyenne glissante

Une moyenne glissante d'un signal $ u(t) $ $u (t)$ , c'est un autre signal$ u_{m}(t) $ dont les valeurs sont obtenues en faisant la moyenne de$ u(t) $ $u (t)$ sur une plage de grandeur plus ou moins grande.

Mathématiquement, si on choisit une plage de largeur totale $T$ :

$ u_{m}(t) = \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}}{u(t-\tau)d\tau} $

Vous aurez peut-être remarqué que l'on peut écrire ça sous la forme de la convolution du signal $ u $ avec une porte d'épaisseur $T$ et de hauteur $1 / T$ (vérifiez ce que je vous dis en remplaçant $u_{2}$ par $u$ $ u $ et $u_{1}$ par la porte $\frac{1}{T} Π (t / T)$ $ \frac{1}{T}Π(t/T) $ dans la définition mathématique de la convolution).

Si vous vous posez des questions sur l'importance de l'ordre des fonctions dans une convolution, sachez que l'ordre n'importe pas puisque :

$ u_{1} \ast u_{2} = u_{2} \ast u_{1} $

Voyons comment cela se traduit visuellement.

Commençons par créer un signal sinusoïdal auquel on ajoute une composante aléatoire :


    %Avant de commencer, un peu de nettoyage
clear all; % efface toutes les variables déjà définies
close all; % ferme toutes les fenètres graphiques
N = 400;
t = linspace(-6,6,N); % créer un vecteur t avec N = 400 valeurs réparties uniforméement
        entre -6 et 6
u = sin(2*pi*0.5*t); %u est un sinus de fréquence 0.5 hz
u = u + randn(1,N); % on rajoute à u une composante aléatoire (Gaussienne)
plot(t,u)

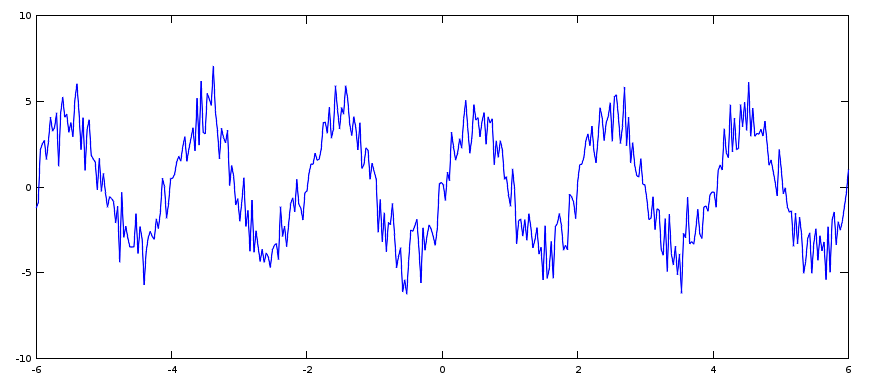
Le signal u oscille sinusoïdalement, mais il a été pollué par des ajouts aléatoires.

Le signal u oscille sinusoïdalement, mais il a été pollué par des ajouts aléatoires.

Nous allons essayer de récupérer la moyenne glissante d'abord avec une petite fenêtre de moyennage, puis avec une fenêtre plus large.

Commençons par une fenêtre petite, c'est-à-dire que nous allons moyenner sur une $\pm 5$ points. Qu'obtient-on ?


    PetiteBoite = ones(1,11)/11; % on va moyenner sur une zone qui va de -5 à +5, soit 11 points en comptant celui du milieu.
u_m1 = conv(u,PetiteBoite,'same'); % l'argument 'same' assure que la taille du signal de sortie est la même que le signal
        d'entrée u
line(t,u_m1,'color','r'); %line et plot fonctionnent un peu pareil, sauf que line évite d'avoir a utiliser "hold on' (plot efface tout par défaut), mais line a moins d'options que plot

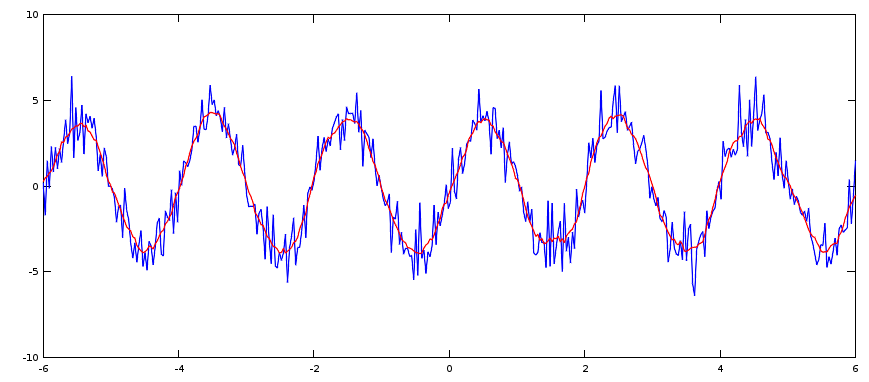
En rouge le résultat de la convolution du signal bleu avec une porte de 11 points de large.

En rouge le résultat de la convolution du signal bleu avec une porte de 11 points de large.

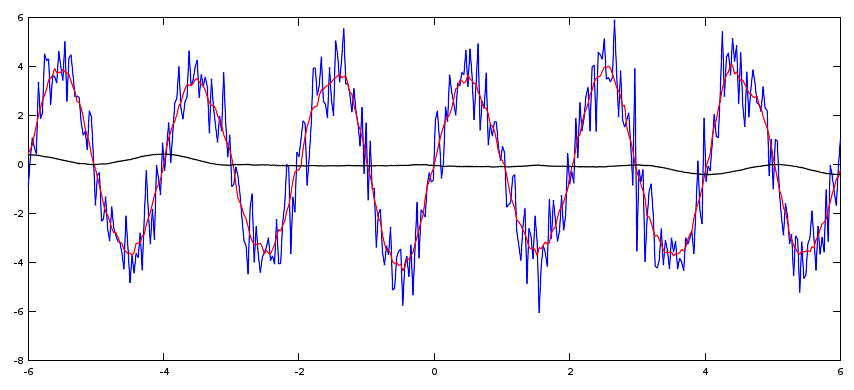
En noir, la moyenne glissante sur une fenêtre très large. Cette fois on ne voit même plus les oscillations, car on a moyenné sur une très large fenêtre.

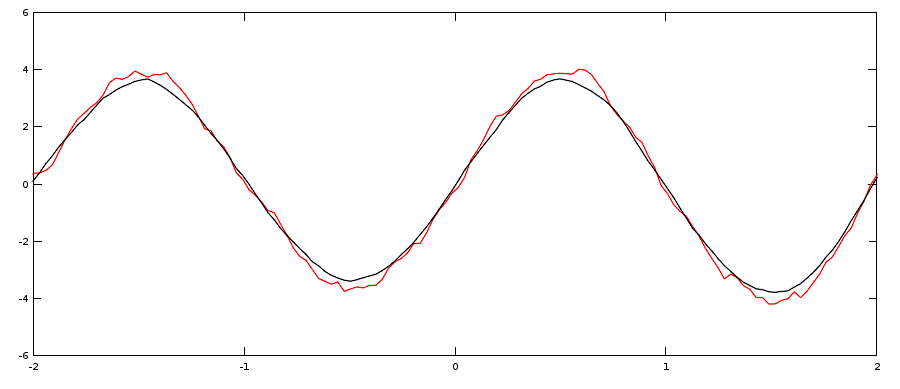
Comparaison entre une valeur moyenne (convolution par une porte, en rouge). Et un lissage (convolution par une gaussienne, en noir). Le lissage est plus doux.

Il existe tout un tas de forme de "filtres" que vous pouvez utiliser pour lisser les signaux (Gaussienne, demi sinusoïde, etc). Vous pouvez jeter un œil à l'aide de la commande fspecial pour voir les différentes possibilités.

Conclusion

Vous venez de voir ce que faisait cette convolution. Dans le chapitre suivant, vous allez voir le lien qu'il existe avec la transformée de Fourier.

À retenir :

La convolution est un outil qui prend deux signaux (qui dépendent du temps) et qui en renvoie un nouveau.
La convolution correspond visuellement à recopier un signal sur un autre.
La convolution est l'outil de choix pour obtenir :

une moyenne glissante ;
un lissage.

Navigation

Analysez les signaux 1D