Réalisez un additionneur à n bits

Nous allons additionner trois entrées logiques A, B, C. Le résultat est donné sur deux bits Sum et Carry. Ce circuit s'appelle l'additionneur complet (full adder). L'interprétation en nombre entier du résultat est donné dans la colonne Result, en combinant Sum comme poids faible et Carry comme poids fort.

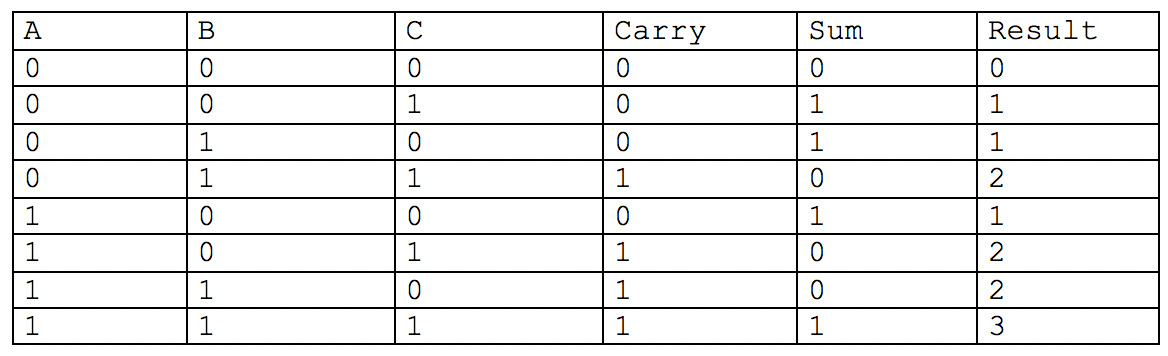
Pour réaliser le circuit arithmétique correspondant à base de portes logiques, vous devez mettre en équation la table de vérité, c'est-à-dire le Carry et la Sum.

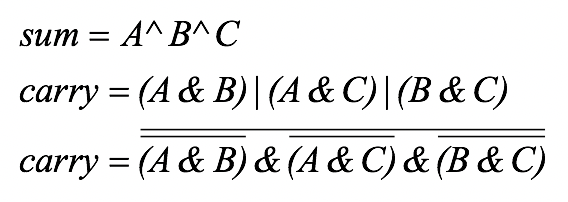
L'implémentation des équations de Sum et Carry à partir de la mise en équation est donnée ci-dessous.

Comme expliqué au chapitre 5, l'outil DSCH vous permet d'encapsuler l'additionneur complet sous forme d'une boîte qui fonctionne exactement comme le schéma initial et qui contient trois entrées A, B et C, et deux sorties Sum et Carry.

Dans cette section, vous allez concevoir un circuit permettant l'addition de deux entiers non signés de 4 bits, A[0..3] et B[0..3].

La conception de cet additionneur est abordée dans son approche la plus simple, où la retenue d'un étage se propage en tant qu'entrée de l'étage suivant. Il se compose d'un demi-additionneur (half adder) pour les bits a(0) et b(0) et de 3 additionneurs complets (full adder) pour les bits de rang 1 à 3.

Le circuit logique illustré ci-après permet l'addition de quatre bits entre deux nombres A[0..3] et B[0..3]. Dans DSCH, les nombres A[0..3] et B[0..3] sont générés directement par des symboles "clavier", ce qui produit une valeur logique de 4 bits correspondant à la touche utilisée.

Dans l'exemple présenté ci-dessous, la valeur de A[0..3]  vaut 1 ( c'est-à-dire 0x1 en hexadécimal et 0b0001 en binaire) et la valeur de B[0..3] vaut F (c'est-à-dire 0xF en hexadécimal, 0b1111 en forme binaire ou 15 en décimal).

Le résultat Sum, qui combine Sum[0], Sum[1], Sum[2], Sum[3] et le dernier bit de retenue Carry, est égal à 0x10 en hexadécimal ou 16 en décimal, ou encore 0b10000.

Avec DSCH, il existe 4 modes de représentation de l'afficheur : hexadécimal, entier non signé, entier, virgule fixe. Pour changer le mode d'affichage, double-cliquez à l'intérieur du symbole et changez le format dans la fenêtre de propriétés du symbole, comme illustré ci-dessous. Le format par défaut des afficheurs est le format hexadécimal.

Dans ce chapitre, vous avez appris à additionner des nombres entiers signés de n bits puis vous avez conçu un additionneur n bits. Dans le chapitre suivant, vous réutiliserez cet additionneur pour réaliser un circuit soustracteur.