7.3 : Le surplus du consommateur
| Site: | Moodle Université Numérique |
| Cours: | Microéconomie 1 : Les décisions du producteur et du consommateur |
| Livre: | 7.3 : Le surplus du consommateur |
| Imprimé par: | Visiteur anonyme |
| Date: | mercredi 11 février 2026, 02:35 |
1. Définitions du surplus du consommateur
Le surplus brut du consommateur est le gain que retire ce consommateur de la consommation d'une certaine quantité (sans prendre en compte le prix qu'il paie).
Ce surplus est calculé en considérant la disposition à payer du consommateur pour chacune des unités de bien qu'il consomme.
Le surplus net du consommateur est égal au surplus brut moins le prix total payé (c'est-à dire en général moins un prix unitaire multiplié par la quantité achetée).
On définit de la même façon le surplus brut de consommation, pour l'ensemble des consommateurs sur le marché : il s'agit de la somme des surplus bruts individuels.
Le surplus net de consommation, pour l'ensemble des consommateurs, est simplement la somme des surplus nets individuels.
Les représentations mathématiques par intégrale et graphiques qui suivent sont valables pour la demande individuelle, mais sont aussi valables pour la demande globale. Il suffit de considérer la demande globale au lieu de la demande individuelle.
2. Remarque sur la demande globale et exemple
Sur une courbe de demande globale, les dispositions à payer pour la 1ère, la 2ème, la 3ème … unités sont classées de la plus grande à la plus petite, quel que soit le consommateur qui est prêt à payer le plus. L’identité du consommateur n’a pas d’importance.
Le surplus global est donc calculé pour l'ensemble des consommateurs, sans se préoccuper de qui consomme et qui ne consomme pas.
Exemple : (il y avait une erreur dans la 1ère version postée sur le site, voici la correction)
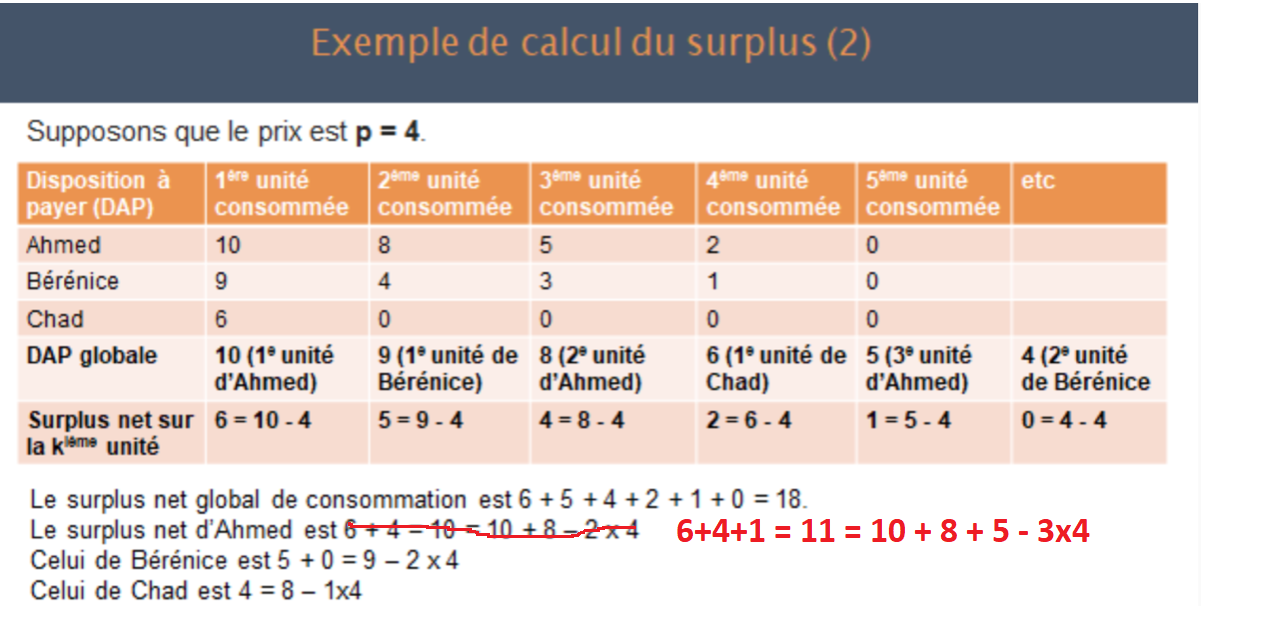
3. Définition mathématique du surplus
Mathématiquement :
Rappel : En équilibre partiel, l'utilité de l'individu dépend de deux "biens", le bien que l'on étudie et l'argent (qui représente la valeur de tous les autres biens que l'on pourrait consommer). On peut donc écrire l'utilité de l'individu quand il a un revenu R et qu'il consomme une quantité x comme : U(x, R - px).
Le premier argument de la fonction est la quantité consommée, x, et le deuxième est l'argent qui reste une fois qu'on a payé l'achat x (cet argent servira à acheter tous les autres biens du panier de consommation de l'agent).
Le surplus net du consommateur, noté SN, est l’avantage que ce consommateur retire en participant au marché et en consommant une quantité x. Ce surplus est mesuré en argent.
Si l'individu achète x unités au prix p, il obtient une utilité U(x, R - p x) = v(x) - p x +R.
S'il ne consomme pas, il obtient une utilité U(0, R) = v(0) - 0 + R.
Le gain net à consommer une quantité x au prix unitaire p est donc la différence :
SN(x) = U(x, R - p x) - U(0,R) = v(x) - p x +R - (v(0) - 0 + R) = v(x) - v(0) - p x.
- Le revenu R s'élimine, le surplus net ne dépend donc pas du revenu mais uniquement de la quantité consommée et du prix.
- On peut normaliser v(0) à 0 puisque c'est une constante qui n'a pas d'impact sur l'analyse. On obtient donc
SN(x) = v(x) - p x.
On peut aussi écrire le surplus sous la forme d'une intégrale :
Le surplus brut est v(x) - v(0) = \( \int_{0}^{x}{v'(z)dz} \)
Le surplus net est SN(x) = \( \int_{0}^{x}{v'(z)dz} \) - px
=
4. Représentation graphique du surplus
On a vu que le surplus net peut s'écrire comme une intégrale. On retrouve ce résultat graphiquement.